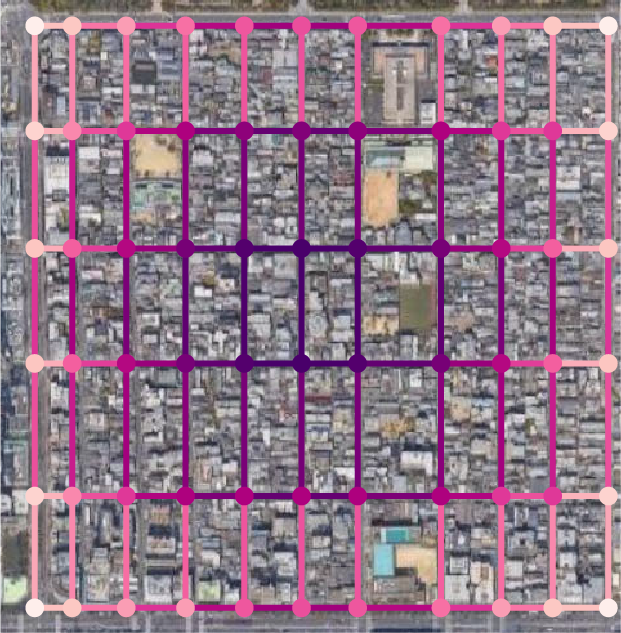
A centrality measure for grid street network considering sequential route choice behaviour
This study proposes a novel centrality measure for a grid network based on pedestrians’ sequential route choices, which we call sequential choice betweenness centrality (SCBC). Although conventional centralities are popular tools for urban network analysis, we must be aware of their meaning in the context of urban planning. This study reinterprets the centralities at the point of pedestrian flow. We then formulate the pedestrian flow distribution based on sequential route choice and develop the SCBC as a function of the probability of going straight at an intersection. The sensitivity analysis shows the probability of minimising the difference between the SCBC and existing centralities while revealing the numerical and spatial features of the SCBC. The more biased the grid proportion, the less similar the SCBC is to the existing ones. Moreover, the SCBC tends to be larger than conventional centralities around the corner nodes of the grid network. The probability parameterises the SCBC to go straight and is related to the pedestrian’s environmental cognition level. This parameterisation enabled us to adapt to the expected pedestrian attribution and perform an in-depth analysis of street networks.

Trade-off of networks on weighted space analyzed via a method mimicking human walking track superposition
This study proposes a method for constructing networks with a small total weighted length and total detour rate by mimicking human walking track superposition. The present study aims to contribute to the scarce literature on multiple objectives, the total weighted length and the total detour rate, by allowing branching vertices on weighted space. The weight on space represents the spatial difference in the implementation cost, such as buildings, terrains, and land price. In modern society, we need to design a new transportation network while considering these constraints so that the network has a low total weighted length that enables a low implementation cost and a low total detour rate that leads to high efficiency. This study contributes to this requirement. The proposed method outputs solutions with various combinations of the total weighted length and the total detour rate. It approximates the Pareto frontier by connecting inherent non-dominated solutions. This approximation enables the analysis of the relationship between the weighted space and the limit of effective networks the space can generate quantitatively. Several experiments are carried out, and the result infers that the area with a huge weight significantly affects the trade-off relationship between the total weighted length and the total detour rate. Quantitatively revealing the trade-off relationship between the total weighted length and the total detour rate is helpful in managerial situations under certain constraints, including the budget, needed operational performance, and so on.

Method for constructing cost-effective networks by mimicking human walking track superposition
Infrastructure networks play a key role in supporting modern city activities. Future technologies will require networks such as hydrogen fuel pipelines and quantum internet networks, which should be feasible and sustainable. This study proposes a method that connects given demand points by a cost-effective network, which has a low total length that enables a low construction cost and a low total detour rate that leads to high operational effectiveness. The proposed method configures the network from scratch by mimicking human walking track superposition on a green space. Walking tracks are expected to be cost-effective because of the self-organization of pedestrians walking on a short path and a path on which others have walked. The resulting networks are equivalent to or more cost-effective than proximity graphs considered cost-effective and have geometric features similar to and different from them. The method requires two dominant parameters: initial walking resistance and ground vegetation recovery speed. A large number of networks with varying parameters approximate Pareto solutions between cost and effectiveness. Increasing either parameter generates a network with a smaller total length and a larger total detour rate. This adjustability is convenient for decision-makers faced with constraints of the construction cost and operational effectiveness.

ランダムドロネー網を用いた重み付きシュタイナー問題の発見的解法
本研究は重み付きシュタイナー問題の発見的解法を開発する．重み付きシュタイナー問題は平面上の与点を連結するグラフの辺の総コストを最小化する問題である．本研究で構築する解法は，ランダムドロネー網を用いて連続平面を離散化し，与点のボロノイ図の双対グラフに含まれる全域木を探索する．木の辺は，ランダムドロネー網上の重み付き最短路で与えられる．近似解の形状と解の総コストの観点から，本手法が既往の重み付きシュタイナー木の発見的解法より厳密解に近い解が得られることを示す．さらに，重みの変化に対する木の形状の不連続な変化を把握する．最後に本手法を，新たな旅客，貨物輸送手段として期待されている大型ドローンの航空路網に適用し，本手法の実用性を検証する．

Desire pathの再現に基づく歩行環境が歩行軌跡に与える影響の解明
本研究の目的は，Desire pathの発生モデルを構築し，歩行環境が歩行軌跡に与える影響を解明することである。Desire pathは草地や土の地面において，人が繰り返し歩行することによって発生するが，美観や衛生の観点から，管理運営上Desire pathを発生させない計画が望まれる．そこで本研究は，地面の仕上げに応じた移動抵抗を加味したランダムドロネー網上での最短路上にDesire pathを再現することで，草や土の領域の移動抵抗を推定し，歩行環境が歩行軌跡に与える影響を解明した．分析より，草の移動抵抗はフォーマルな空間やパブリックな空間ほど大きく，インフォーマルな空間やプライベートな空間ほど小さいこと，土の移動抵抗は舗装路の移動抵抗とほぼ同一であることが明らかになった．